CS 3540: Programming Languages and Paradigms

Random Thoughts On the Way to Class

Many of the lists we work with in programming are, in principle, very long or even infinite. The log output from a web server will row as long as we let it grow, beyond any fixed limit. So will the stream of Instagram posts we see. The number of digits of pi is infinite. So is the list of integers, the list of even numbers, and the list of prime numbers.

Yet, when we model these ideas in our programs, we usually stuff them into data structures with fixed limits on their size.

In general, we like for our programs to model things in the world as faithfully as possible. It would be more faithful if we could model a web server's log or a stream of tweets or a list of integers as unbounded in length.

We need an infinite data structure.

An Opening Exercise

So I ask you:

> (define evens (infinite-list ...))
> (first evens)
0
> (first (rest evens))
2
> (first (rest (rest evens)))
4
> (first (rest (rest (rest evens))))
6
> (first ((skip 7) evens))          ; (skip n) calls rest n times for me
14
> (first ((skip 1278714) evens))
2557428

Hint 1. We have used inductive definitions to describe infinite sets of values in the past. For example, the set of non-negative integers can be defined as:

• 0 is in the set.
• If n is in the set, then n + 1 is in the set.

Those correspond to zero and succ in the API for the integers we saw last time. Can you use this idea in your code?

Hint 2. The inductive part of that definition looks a bit like a function. Last time, we saw that we could implement a data value using a function. Can you use this idea in your code?

Infinite List as Data Abstraction

Infinite lists are not a primitive type in Racket, but we can implement them as a data abstraction. We might try any of the implementation styles we saw last session implementing the pair ADT, but I think that we'll need to use a functional abstraction of some sort for an infinite list. Obviously, we can't store an infinite number of values. But if, instead, an infinite list knew how to generate the rest of its values, we might be able to implement an infinite list in a finite piece of code!

How about if we use the idea of an inductive definition to model an infinite list as a pair? After all, a list is a pair whose cdr is a list. The pair will contain:

• a number k that is in the set, and
• a function that uses k to generate the next member of the set.

Check out this solution to see one implementation. The hard work implementing this data type comes in the rest function, which has to compute the next value in the list and assemble a new integer/function pair.

That file also shows how we can generalize the take function to work with infinite lists. (My skip function does something similar to what drop does for regular lists.)

Spend a couple of minutes looking at how take-using uses letrec to create and return a recursive function. This is a handy programming pattern.

We can treat functions as data...   We can implement data using functions...   I hope that you are beginning to see a pattern emerge. The idea is powerful.

By the way, in some languages, such as Haskell, the infinite list is a language primitive! Consider:

[1..]               defines the list of positive integers
[1,3..]             defines the list of odd integers
filter odd [1..]    also defines the list of odd integers

Haskell accomplishes this and many other cool things by being lazy: it does not evaluate arguments passed to functions until they are used. Clojure, a language that looks a lot like Racket, has a macro facility for lazy sequences. We could do the same thing in Racket by creating new syntax for a data abstraction.

Python provides an operator called yield that enables us to create "generator" functions of the sort I cobbled together for infinite lists. Ruby and many other languages provide yield or something similar. Racket defines a lambda-like operator for generators in its racket/generator library. If you'd like to see how these work, check out this Python example and this Racket example.

Data Abstraction

As you undoubtedly learned in your data structures course, data abstraction plays an important role in the construction of maintainable, correct code. There are at least two reasons for the benefits of an abstract data type (ADT).

First, an ADT enables us to write client code in terms of the abstraction, rather than in terms of its implementation.

Consider the set ADT we encountered in Session 19 as part of the free-vars function. The functions set-member?, set-add, and set-union allow us to write code about sets, which are not native to Racket. Programmers can use the ADT to program using their existing knowledge of sets without worrying about how to make sets "work" as Racket lists. The result is client code that easier to read — and write.

Any time we bypass the ADT and refer to an implementation detail, we risk breaking code. This is as easy to do as returning () as an empty set, instead of the ADT's the-empty-set value.

We use syntax procedures for the same reason. A function such as free-vars or occurs-bound? are about an idea that is independent of how programs in our little language are represented. That representation should not show up in our code. Syntax procedures make client code read as if our program is manipulating data that are built into Racket. They remove unnecessary clutter from programmers' minds as they write the code.

Syntax procedures hide the underlying representation of programs, which highlights a second benefit of ADTs: by erecting a wall between the users of a data type and its implementation, an ADT makes it possible to change the implementation of the data type without affecting client code. If only the functions in the public interface know and use the ADT's internal implementation, then we can change the implementation without changing the client code.

To this point in our discussion of data abstractions, the abstract data types we have implemented in Racket offer the first of these benefits but not the second. All of our ADTs have been transparent: Users of our sets can see through to the implementation and treat them as lists. Some of you have done so in your own homework solutions, writing caadr instead of lambda->parameter, for instance. The problem is that our abstractions have been unenforceable.

Soon, we will explore a programming language construct called a closure and see how we can use it to create true information hiding in our ADTs. We will also see how to use closures to implement other programming language features.

This session we consider the design choices for a particular ADT, the finite function. Like many things in this course, our discussion serves two purposes. First, it lets explore a data abstraction idea we learned about last time, the idea of using a function to implement a data structure. Second, it introduces us to a data structure that we need in order to build a language interpreter: a way to store variables and their values, which in programming languages is called an environment.

Finite Functions

Your reading assignment for today reminds you that a function is a mapping from values in one set, the domain, to values in another set, the range. Each value in the domain may be associated with at most one value in the range. That is, for each value in the domain, there is a unique value in the range.

In mathematical terms, a function is a set of ordered pairs. In computing, we can implement a function as a set of ordered pairs. We can also implement it using some other data structure, as long as the function preserves the essential behavior of a function.

In computer programming, though, we also think of a function as a piece of code that can be evaluated (behavior). We can implement a mathematical function using a computer function, too — as long as the function preserves the essential behavior of a function.

A finite function is a function that has a finite domain. A finite function can always be written as a finite set of ordered pairs, though in practice this is often tedious or impractical. For example:

f = {(foo, 2) (bar, 5) (baz, 15)}

is a finite function. It consists of three ordered pairs. If f contained 500 pairs, then we might not want to write it down by hand!

In Python, we might use a dictionary to implement a function. For example:

> ff = {}
> ff['foo'] = 2
> ff['bar'] = 5
> ff['baz'] = 15

> ff['foo']
2
> ff['bif']
[...] KeyError: 'bif'

> ff['bif'] = 27
> ff['bif']
27

We could also use a Python list of tuples to implement a function: ff = [('foo', 2) ('bar', 5) ('baz', 15)]. If we did, we would use ff.append(('bif', 27))] to add a new pair to the set, rather than use ff['bif'] = 27. We would also need different code to look up the values of 'foo' and 'bif'. Already we can see the need for defining an abstract interface for finite functions.

Finite functions play an important role in computer science because we often want to create mappings between two finite sets of objects.

• Variables must be bound to their values in the current scope.
• Java messages must be matched with methods at run time.
• A compiler might, during its scanning phase, create a table that maps every token in a program to the set of locations at which it appears.

Many languages include primitive data types that can play this role, including Racket and Python.

Let's implement finite functions for ourselves. Our implementations will be lightweight and perfect for use in our interpreters. Implementing them will also expose how they work.

But how to implement it? Our discussion above tells us that there are at least two different ways: functions and data.

Representing Finite Functions as Racket Functions

One straightforward representation of finite functions uses a function to compute the value of any item in the finite function's domain. So, to represent f = {(foo, 2) (bar, 5) (baz, 15)}, we might use the following function:

(define f
  (lambda (arg)
    (cond ((eq? arg 'foo) 2)
          ((eq? arg 'bar) 5)
          ((eq? arg 'baz) 15)
          (else (error 'ff
                  "argument not in domain -- ~a" arg)))))

This looks as much like a "function" as anything we've written this semester!

But where is the data structure?

Writing a finite function in this way works best when a human programmer writes the code for a finite function, and all of the pairs in the finite function are known at programming time.

But we most often want to use finite functions within a running program that is "discovering" the set of pairs as it processes its input. For example, we might need to build a list of variables within a lexical-address function as it traverses an expression. Thus we will want to have lexical-address build the finite function in a piecemeal fashion as it encounters new variable bindings.

How might we write code to do that? We can describe finite functions inductively. For example, we can construct the function {(foo, 2), (bar, 5) (baz, 15)} by adding the mapping (bar, 5) to the set {(foo, 2), (baz, 15)}. We usually refer to this as extending one function to create another.

Keep in mind, though, that these are sets, so the order that the pairs appear in the function does not matter. We could just as easily create {(foo, 2), (bar, 5), (baz, 15)} by adding the mapping (foo, 2) to the function {(baz, 15), (bar, 5)}.

To add the pair (bif, 27) to f, we can define a new function as:

(lambda (arg)
  (cond ((eq? arg 'bif) 27)
        (else (f arg))))

This function uses f to handle the original three pairs and handles the fourth by itself.

My new function "hardcodes" the finite function that was extended in it body. But in the course of running a program, we don't usually know the specific function to call. To extend any existing finite function, let's create a function that tests for values in the domain of the extension and calls the original function for all other arguments. For example, this function extends any finite function with the pair (bif, 27):

(define extend-with-bif
  (lambda (ff)                      ; receive a finite function
    (lambda (arg)                   ; and create a new function
      (cond ((eq? arg 'bif) 27)     ; with (bif, 27)
            (else (ff arg))))))     ; and the original

Great. But this is still ad hoc... It hardcodes the new symbol/value pair in its body. How can we write code that another programmer could use to write programs that grow and use finite functions over time? Let's build an ADT.

Representing Finite Functions as Racket Functions, API Version

We can do finite functions inductively:

finite-function ::= empty-function
                  | finite-function + new symbol/value pair

First of all, we can think of every finite function as an extension of the empty function, so we create a constructor for the empty function:

(define empty-ff
  (lambda ()
    (lambda (sym)
      (error 'ff
              "argument not in domain -- ~a" sym))))

Why make this a function, rather than a data value? Because in this implementation, a finite function is a Racket function. It takes an input value and returns an output value. Why signal an error? Because the empty function is, well, empty. This means that its domain is empty, and so the function cannot return a value for any input it is given.

Then, we make it possible to extend a finite function, much as we did above, but this time with all three values taken as arguments:

(define extend-ff
  (lambda (sym val ff)
    (lambda (symbol)
      (if (eq? symbol sym) 
          val 
          (apply-ff ff symbol)))))

To complete the abstraction, we define apply-ff, the function that applies a finite function to an argument.

(define apply-ff
  (lambda (ff symbol) 
    (ff symbol)))

Why define apply-ff at all? In this implementation, a finite function is a Racket function. We can simply call it, just as we call any Racket function, by applying it to an argument:

> (my-ff 'bar)
5

This is a good example of where a programmer must take care to define a complete ADT. In this implementation, a finite function is a Racket function, but we can implement the idea in many ways. We are defining an abstract data type, and Racket functions just happen to be the way we are implementing the ADT today. What happens when we want to change the implementation next session?

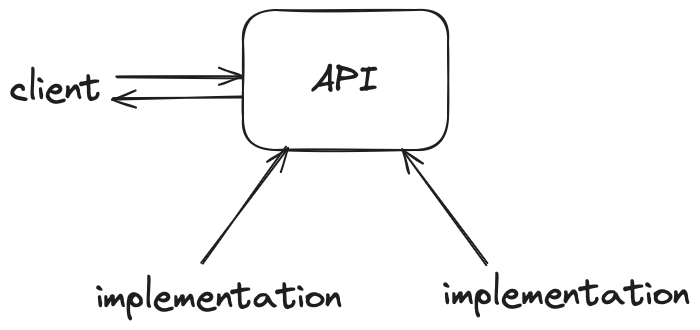
In the software world these days, we often hear about APIs, which is short for application programming interface. an API is a broader idea than an ADT, but they are similar in at least one respect. Designing a complete API is a challenge for any language developer and any programmer who builds new services. Separating the definition from the implementation is also essential, for just the reasons it matters to us here.

Without apply-ff, we would have committed ourselves to using functions to implement finite functions. We would never be able to change that part of the implementation — without having to modify every client function that uses a finite function. Without apply-ff, every client function would have to know to look up values of the function by applying the finite function as a Racket function. This would commit not only us to a particular implementation, but every programmer who ever uses the ADT.

If this seems nit-picky now, it should become clearer as we re-define finite functions using alternative data representations... Oh, and will we!

So now we have a defined finite functions as an ADT with three operations:

(empty-ff)              -> empty finite function
(extend-ff sym val ff)  -> a finite function extended with (sym, val)
(apply-ff ff sym)       -> the value associated with sym in ff

Using this implementation of finite functions, we can now create the finite function {(foo, 2) (bar, 5) (baz, 15)} with the following code:

(define my-ff
  (extend-ff 'foo 2
    (extend-ff 'bar 5
      (extend-ff 'baz 15
        (empty-ff) ))))

Does it work?

> (apply-ff my-ff 'foo)
2
> (apply-ff my-ff 'bar)
5
> (apply-ff my-ff 'baz)
15
> (apply-ff my-ff 'bif)
finite-function: argument not in domain -- bif

What does my-ff look like? Use the substitution model to figure it out! Then check out the results of my program derivation in this code file.

An Exercise: Adding Multiple Extensions at Once

Now that we have written extend-ff and empty-ff, we can write recursive functions that build and use finite functions. Often, though, we will encounter several new variable/value pairs at once, rather than individually. For example, a Racket lambda expression may bind several arguments to several parameters, all at once. Extending a finite function one binding at a time would result in ungainly, ugly code. However, we could build a function to handle multiple extensions cleanly.

(extend-ff* sym-list val-list ff)

> (define boo (extend-ff* '(foo fiz foz) '(1 4 9) (empty-ff)))
> (apply-ff boo 'fiz)
4

> (define new-boo (extend-ff* '(hey hee) '(16 25) boo))
> (apply-ff new-boo 'fiz)
4
> (apply-ff new-boo 'hey)
16
> (apply-ff new-boo 'bam)
finite-function: no such key -- bam

How can structural recursion help you?

A Possible Implementation

Structural recursion can help you in this way. The arguments to extend-ff* are two lists of the same length. So you can implement your function recursively using the inductive definition of a list, by making repeated calls to extend-ff with a single variable/value mapping taken from the two argument lists.

After trying to write the function yourself, take a look at one possible solution. The implementation uses straightforward structural recursion over a list. extend-ff* computes an extended finite function for the cdr of the list and then passes it on as an argument for making a single extension for the car via extend-ff. This is another example of "double" recursion, as the function walks down the two lists together, one item at a time.

This also illustrates the idea we have just been studying... extend-ff* is a syntactic abstraction of extend-ff! It isn't necessary, but it does make client code easier to write. In particular, it iterates over a collection, meaning that client code doesn't need a loop or recursion to handle multiple extensions.

Study the idea of a finite function. We will use this data type later in the semester. Study, too, our procedural implementation. Next session, we will see how functions can be use in different contexts to create programs that have state!

Next Time: What You've All Been Waiting For

We will consider I/O, sequences of statements, and even assignment statements. How much do you miss them, really, though?

Homework 9

The new homework assignment is available. It is the first of three stages in building an interpreter for a small language that works with colors. You will extend this code on Homeworks 10 and 11. As a result, it's worth a little extra effort to write good, clean code for this assignment.

The assignment consists of two main functions, plus a set of syntax procedures for the language. You will produce a lot of code for Problem 1, but keep in mind that you can copy, paste, edit code from one kind of expression to the next.

Even more than usual, I strongly encourage you start this assignment early. Study the specification of the language that we are implementing so that you understand it as well as possible before you start writing code. Ask questions about both the language spec and the homework problems early.

Wrap Up

• Reading
  • Review the lecture notes and code for today's session.
  • Prepare for next time by reading a short section on imperative programming in Racket. Try the code, too!
• Homework
  • Homework 9 is available and due next week.
• Quiz
  • I returned Quiz 3 at the end of class.