Mathematical Functions
A Brief Refresher on Functions
In computer programming, we speak often of functions. Have you ever wondered about the relationship between functions in computer programming and the functions you learned about in math class back in grade school?
You all know what a function in computer programming is: a piece of code that, for a given input value, returns an output value. All of the Racket functions we've written this semester work this way, for example:
(define (square n) (* n n))
We can think of a program's function as a machine that converts input values into output values:
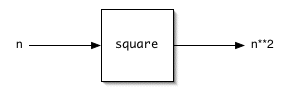
In our math classes, we would have written this as:
f(n) = n2
In math, a function is a mapping from values in one set, the domain, to values in another set, the range. Each value in the domain may be associated with at most one value in the range. That is, for each value in the domain, there is a unique value in the range.
This has been true of all the functions in our programs this
semester, too. One of Racket's primitive "function" thus far has
behaved differently: random. It returns a
different value each time it is called. This is one
of the reasons sub-programs in Racket are more precisely called
procedures rather than functions: they do not have
to return a unique value for a given input.
In mathematics, a functions is often represented as a set of ordered pairs, for example:
f = {(1, 1) (2, 4) (3, 9)}
f = {(foo, 2) (bar, 5) (baz, 15)}
If two pairs in the set have the same first value, then the set is not a function; it is a relation. A function is a relation, but not vice versa.
Some functions are infinite sets. Their domains are infinite sets. For such functions, we often define a rule that describes the mapping from domain to range. For example, the set:
f = { (x, y) | x is a real number and y is x² }
is an infinite function. Indeed, it is the mathematical function
that corresponds to our square procedure above!
So: a function in math and a function in a program can and often do describe the same set of mappings. One is a data value (a set), and the other is a procedure. What does this suggest to you?
Finite Functions
A finite function is a function that has a finite domain. (By inference, it also has a finite range.) A finite function can always be written as a finite set of ordered pairs, though in practice this is often tedious or impractical. For example,
f = {(foo, 2) (bar, 5) (baz, 15)}
is a finite function. If f contained 500 pairs,
then we might not want to write it down by hand!
Finite functions play an important role in computer science because we often want to create mappings between two finite sets of objects.
- Variables must be bound to their values in the current scope.
- Java messages must be matched with methods at run time.
- A compiler might, during its scanning phase, create a table that maps every token in a program to the set of locations at which it appears.
More generally, many modern languages provide finite functions as
a primitive data type. For example, Python defines
a dictionary datatype,
and Java defines
a Map interface
for its many classes that map keys to values. You might think of
such data structures as generalized arrays, where the index is
not limited to being a non-negative integer. The index can be an
arbitrary object. The rise of scripting languages such as Python,
Perl,
and
Ruby
have made finite functions a workhorse of modern programming, in
the form of hashes and dictionaries.
With finite functions being so useful to us in computer science, it is not surprising that we will want to use them in our language processors. Scheme is a minimal language and does not provide this data type as a primitive. Racket offers a hash that can be used as a finite function. Let's implement the data type for ourselves, so that we can see how it works. Our implementations will be lightweight and perfect for use in our interpreters.
But how to implement it? Our discussion above tells us that there are at least two different ways: functions and data. Next session, we will begin to explores these options.