CS 4550: Translation of Programming Languages

Session 23
Generating Three-Address Code

Recap

We are now considering the synthesis phase of the compiler, which converts a semantically-valid abstract syntax tree into an equivalent program in the target language. In our last session, we introduced the idea of intermediate representation, looked at a couple of candidate intermediate representations, and settled on a third — three-address code — that serves as an especially useful point for us on the way to machine-level code.

Statements in three-address code are patterned on the general form x := y op z, with at most three identifier addresses. Three-address code requires the code generator to introduce temporary identifiers in order to decompose more complex expressions, including control structures. The essence of this stage of processing is that it linearizes the AST in a way that prepares for generating target code.

Today, we:

Designing a Three-Address Code Language

As you can see, three-address code resembles assembly language in its level of expression. The expressiveness of a three-address code language depends on the number and kind of statements allowed.

Basic Operations

In particular, any useful three-address code language will likely have these basic operations:

  • binary assignments of the form x := y op z. The language must define a suitable set of arithmetic and boolean operators.
  • unary assignments of the form x := op y. Unary operators may include not only arithmetic and boolean operators but also shift and type conversion operators.
  • copy assignments of the form x := y, simplest of all.

Flow of Control

To support flow of control, it will likely have:

  • unconditional jumps of the form goto x, where x is a label in the program.
  • conditional jumps of the more general form if x op y goto z, where op is a boolean operator and z is a label in the program.
  • a set of statements for higher-level transfers of control such as procedure calls. This set might contain the forms:
    • param x, where x is the location of a parameter,
    • call x y, where x is the location of a code segment to execute (the procedure body) and y is the number of arguments to the procedure, and
    • receive x, where x is the location of the value returned to the calling code.
    It might be handy to have instructions such as begin_call and end_call, too. They aren't strictly necessary for human readers of 3AC, but they can represent the calling and return sequences that every function call must generate!
  • labels of the form label x, which create a label in the program named x.

After our last few sessions working with TM, you may already see ways in which these control flow operators would follow from Klein code and lead to TM code.

Higher-Level Data Types

Finally, in order to represent higher-level data types such as arrays and pointers, it might have:

  • indexed assignments of the forms x := y[z] and x[y] := z, where [] is the subscript operator.
  • address assignments of the forms x := &y and x := *y, where & is a unary operator that returns the address of its argument and * is a unary operator that returns the value at the address specified by its argument.

Final Notes

A three-address code (3AC) language for representing C programs would require all of these expressions. A 3AC language for Klein can be smaller.

Writing 3AC program typically results in many temporary variables, to hold the results all of the intermediate results created by teasing apart a more complicated expression.

The 3AC language described above is merely an example of the kinds of expressions that a compiler will need for a simple language. We are free to create the kinds of operators that will be most useful for the source and target languages of our compiler.

The design of a three-address code — and especially its set of unary and binary operators — has a large effect on the resulting code generator. As mentioned above, the intermediate language must be rich enough to implement the semantics of the source language. Beyond that, we must strike a balance between a small-enough language, which is easy to implement and re-target, and a too-small language, which leads to longer three-address code programs. The longer the resulting representation, the harder the optimizer and code generator must work harder to generate an efficient target program.

Exercise: Generating Three-Address Code by Hand

Consider the following Klein expression. It is the body of the remainder function in the euclid program, a part of the standard Klein distribution.

Write a 3AC program for this expression using the 3AC statements described above. 
if (a < b)                (* Line 1 *)
    a                     (* Line 2 *)
else                      (* Line 3 *)
    remainder(a-b, b)     (* Line 4 *)

Remember: the value of the if expression is either the value of the 'then' clause or the value of the 'else' clause. You can use the same temporary variable to store those two results.

For an extra challenge... +

Once we have a fully-specified 3AC language, it will take only a little practice before you can write three-address programs of this sort by hand with little effort — though perhaps much tedium. That tedium will motivate you to write a program that generates 3AC programs for you!

Generating Three-Address Code in a Compiler

So, how can a compiler generate a representation in three-address code? We will use the same technique we used to process the abstract syntax tree in earlier stages of the compiler: walk the tree using structural recursion. For each node in the AST, the code generator writes an equivalent sequence of 3AC statements.

In the compilers world, this sort of processing is often referred to as syntax-directed translation. Some of the issues we will want to consider in implementing syntax-directed translation include:

Let's look at the first three of these in this session and consider higher-order structures next time.

Elements of a Three-Address Code Generation

Each node ni in the abstract syntax tree corresponds to an expression E on the left hand side of a grammar rule. The 3AC statements for the node will compute a value, which is stored into a new temporary variable ti. The representation generated for E will consist of two parts:

Generating three-address code in this way uses many temporary variables. The code generator will need a procedure such as makeNewTemp() to create a new, unique temporary variable name each time it is called. For simplicity, let's assume that we this procedure exists and that it generates the sequence t1, t2, t3, ....

Also for simplicity, we will use a unique identifier for each temporary. A more efficient compiler could use a smaller pool of unique identifiers, reusing the same name multiple times in different scopes.

The code generator also needs to emit code in three-address form. For now, let's assume that we have a procedure named emitCode() that works something like Python's primitive print() function: it takes one or more strings, concatenates them together, and writes the result, followed by a new line character.

In the discussion that follows, we will use emitCode() to generate a string that we can store in an expression's code field. Later, we will look at data structures for holding 3AC statements on their way to generating target code.

When writing your compiler, you can implement your own makeNewTemp() and emitCode() procedures to behave in just these ways, and then use them!

Three-Address Code for a Small Grammar

Suppose that we have the following simple grammar: 

S → id := E
E → E1 + E2
  | E1 * E2
  | - E1
  | ( E1 )
  | id

We likely would have created five kinds of AST node for this grammar: one for each rule except the parenthesized expression rule. In our tree, (E1) would simply be an expression node.

Here is the 3AC-generating action for the first arm of the grammar: 

S → id := E
------------
S.code := [ E.code ]
          emitCode( id.place, " := ", E.place )

The expression [ E.code ] means to look up the 3AC for E, or make a recursive call to compute it, and place it in this location. This is immediately before the code generated by the call to emitCode() that produces the code for the statement itself.

Notice that the top-level grammar rule is a special case. It defines a statement, not an expression, so its left hand symbol does not need a temporary variable associated with its value.

What about the rest of the grammar? We will use the procedures makeNewTemp() and emitCode() to create the semantic actions for generating three-address code for each kind of expression. The result of computing each kind of expression will be stored in a newly-generated temporary variable. The code that performs the computation will be based on the right hand side of the production.

As in most data-driven recursive programming, structural recursion does much of the work. Each semantic action simply packages the code built by the recursive calls with the newly-generated statement, if any, in the correct order.

Here is a possible set of actions for the rest of the grammar: 

E → E1 + E2
------------
E.place := makeNewTemp()
E.code  := [ E1.code ]
           [ E2.code ]
           emitCode( E.place, " := ", E1.place, " + ", E2.place )

E → E1 * E2
------------
E.place := makeNewTemp()
E.code  := [ E1.code ]
           [ E2.code ]
           emitCode( E.place, " := ", E1.place, " * ", E2.place )

E → - E1
---------
E.place := makeNewTemp()
E.code  := [ E1.code ]
           emitCode( E.place, " := negate ", E1.place )

E → ( E1 )
-----------
E.place := E1.place
E.code  := [ E1.code ]

E → id
-------
E.place := id.place
E.code  := ""

The duplication of code in the + and * cases indicates that we can create a single routine to generate 3AC for multiple binary operators. We can do the same for multiple unary operators.

When we implement this code, a programmer-defined identifier is replaced by a pointer to a symbol table entry for the identifier.

In Module 5, we have to process an integer literal. What sort of three-address code do we generate for a literal?

Implementing Three-Address Code

Note. This section goes a little deeper than you are likely to implement in your own three-address code generator. However, you may find it worth a quick read, as it illustrates one of the Big Ideas of computer science and ends in advice you can use on your project.

A statement in three-address code is an abstraction that the compiler writer must implement in code. Rather than generate a text representation for each statement, the compiler could represent each statement as a record with fields for its parts.

What might each three-address code statement look like? There are at least two options.

Quadruples

We could represent each element of a 3AC instruction directly using a quadruple, a record with four fields: the operator, the left operand, the right operand, and the result.

Consider the three-address code for our old friend, the expression a := b*-c + b*-c, using quadruples:

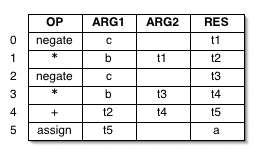
a sample record layout for quadruples

As mentioned earlier, the slots that refer to programmer-defined names can be replaced with pointers to the corresponding symbol table entries.

3AC instructions that deviate from the standard pattern will use a subset of these fields. For example:

  • Unary operators can leave the right operand slot empty.
  • param identifies only a single argument to a procedure, so it can leave both the right operand slot and the result slot empty.
  • Jump instructions do not have results, but they do have target labels. The label can be stored in the result slot.

Note: If you implement these statements using different kinds of object or as variable-length records, then these conventions become unnecessary.

Triples

Notice that using quadruples creates a kind of duplication. Each statement has a result, which is stored in a temporary location. The order in which these temps occur matches the sequence of the statements themselves.

We can eliminate the explicit representation of the temporaries that hold results by storing in the corresponding argument slot the number of the instruction that computes it. The result implements three-address code in a triple.

Here is what a triple representation would look like for our example:

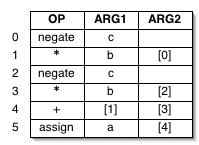
a sample record layout for triples

Note that the record numbers 0 through 4 now stand in place of the five temporary variables, t1 through t5, which eliminates the need for a result field.

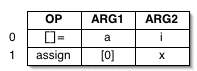
Using triples creates a new wrinkle for statements such as a[i] := x, though. Assigning a value to an array slot requires two separate operations:

  • computing the target slot in the array, and
  • assigning a value into that slot.

Such a statement requires two triples:

ternary operations, such as array slot assignment, require two triples

A Compromise: Indirect Triples

There are some interesting trade-offs between these two representations. Triples are efficient and compact. Quadruples can use a single instruction in some cases where triples require two. Triples are hard to reorder, because many entries refer to other entries by their positions in the list.

Being able to reorder statements is an important feature if we want the compiler to improve the efficiency of the code it generates. We could represent the triples using a linked list, with pointers playing the role of the array's indices. However, that makes the compiler itself less efficient in other ways.

We can stick with an array representation and still find a nice balance between triples and quadruples using a technique known as indirect triples.

The idea is straightforward: the code generator maintains an array of pointers to triples. If it is necessary to reorder instructions, it can reorder the pointers, not the triples themselves.

Indirect triples are an example of one of programming's great lessons, captured in an aphorism attributed to pioneer computer scientist David Wheeler:

All problems in computer science can be solved by another level of indirection.

Your Klein compiler does not demand the extra work needed to implement and use indirect triples.

Final Advice

There is a lesson here for us, even if we don't go as far as using indirect triples. One way to decouple code from a decision is to move the decision elsewhere.

For example, rather than hardcoding values into our code generator for Module 5, we can call a function that returns the value for us. Later, on Module 6, we will add code to the function that does some real work to solve a more general problem.