Session 5 Demo
Converting an NFA to a DFA
Converting a Nondeterministic FSA into a Deterministic FSA
The idea is to simulate the NFA on all possible inputs, creating a compound state [j, k, ...] in the DFA whenever a symbol takes the NFA from state i to one of the states j, k, ..., non-deterministically. Likewise, when we create a transition on a given symbol out of the compound state, we create another compound state [m, n, ...] that includes all of the states reachable from any state in the source state. Any state that contains a final state from the NFA is a final state in the DFA.
Let's try it out on our simple 4-state NFA that recognizes
(a | b)*abb:
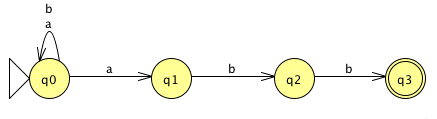
We start with the start node:

From q0, an 'a' takes the NFA either to q0 or q1, so we create a compound state q0q1 in our DFA. A 'b' is simpler, as it keeps the NFA in q0.
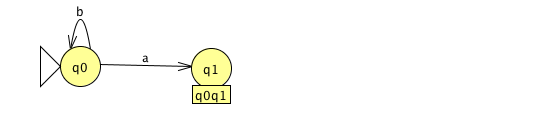
From q0q1, an 'a' takes the NFA either to q0 or q1 (from q0), and nowhere from q1. We already have a state q0q1, so we add a transition. A 'b' takes the NFA either to q0 (from q0) or to q2 (from q1). So we create a new compound state q0q2 in the DFA.
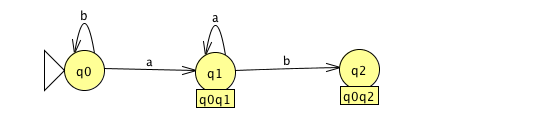
From q0q2, an 'a' takes the NFA either to q0 or q1 (from q0), and nowhere from q2, so we add a transition. A 'b' takes the NFA either to q0 (from q0) or to q3 (from q2). So we create a new compound state q0q3 in the DFA. q3 is a terminal state in the NFA, so q0q3 is a terminal state in the DFA.
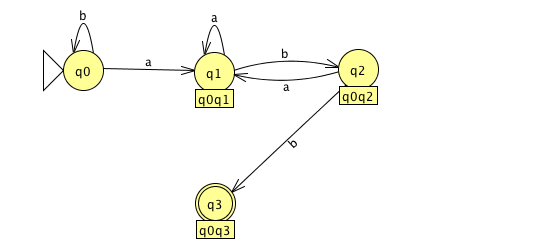
From q0q3, an 'a' takes the NFA either to q0 or q1 (from q0), and nowhere from q3. Again, we add a transition to the existing state. A 'b' takes the NFA to q0 (from q0) and nowhere from q3. So we add a transition back to q0.
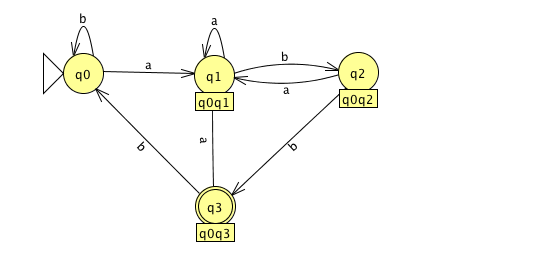
The last step did not add any new nodes, and we have accounted for 'a' and 'b' transitions out of every state in the DFA. We are done! The result is a complete and deterministic FSA with four states: the same number as in the NFA we started with.