Week 14 - A* for Twiddle

A* Search Explained

 

 

A* Romania

Below is complete working code for the A* search that solves the Arad to Bucharest Problem

I began by using the code I created for the Uniform-cost Search last week:

 

In order to make this work, I had to modify the way the PriorityQueue sorted the Nodes on enqueing. I didn't want just the cost so far, I needed a combination of cost so far PLUS the heuristic estimation. So I needed to figure out how to add in the heuristic (the straight line distance table).

 

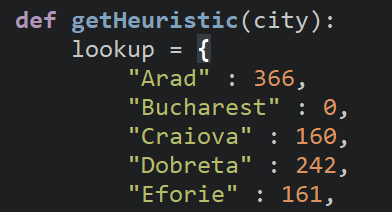
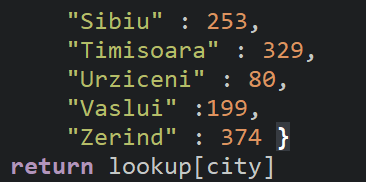
  1. I created a function called getHeuristic that takes in a city as a parameter and returns the straight line distance from that City to Bucharest based on the chart from my slides. [NOTE: This uses a Python dictionary as a lookup table rather than messing with a big messy set of conditionals.]
    • ...

     

  2. Once that was working the way I wanted it, I added it into the Node class and modified it to work with the city that was already part of that Node.

     

  3. Next, we talked in the slides about f(x) = g(x) + h(x) where g(x) is the cost so far (which is stored in self.c in our Node) and h(x) is the heurstic from this city to our goal (which is returned gy getHeuristic()). So I created a function called fValue() that gave that combined score:

     

  4. Modify the __lt__, __gt__, __eq__ magic method to use the fValue() functionwhen sorting the PriorityQueue

 

That's it. All of my changes went into the Node class. Since I changed what numbers were used to sort the Priority Queue by changing the magic methods, the code for the Uniform Cost search worked as is.

 

When you run this code it will produce the same answer as it did when it was the uniformcost solution and you won't honestly know it was any different. But it is. Trust me. If we ran a timer with this you would find that it finished faster and there is less stuff left over in the Frontier when we are done (because it looked at fewer nodes).

This change isn't noticable here, but will be when you try this yourself with Twiddle.

 

 

A* Twiddle

To wrap this all up, I am going to ask you to make a serious effort to program the A* search for the Twiddle puzzle we looked at in week 12. I am going to strongly encourage you to use my ending code from Week 12 rather than your own unless you are fairly confident your code is doing similar things (including the new version of Node that contains a pointer to the parent Node rather than a String representing the parent Node's board. That will be important here).

 

In order to help you conquer this program I'm going to suggest you do it in the following steps which are similar to my steps above.

 

 

The heuristic function

This is really the substance of this whole activity.  It is, arguably, the most time consuming. But if you really think about this problem, it is very manageable.

To do this part I suggest you just work in a new empty file to you can more easily test it, and then move it over to the Node in the next step.

Action:

Create a function called getHeuristic() that takes in a Twiddle board (a length 9 string) and returns a heurstic value of the board based on the modified Manhattan Distance as discussed in the discussion videos.  This score should be the sum of the minimum number of moves required to move/slide each of the 9 numbers, individually, to it's target location, AND THEN the whole thing divided by 4 (since each Twiddle action moves 4 numbers, if we don't divide by 4 we would over estimate which means the result is not admissable).

For example:

Has a value of:

since the numbers are  3 + 2 + 2 + 2+ 1 + 1 + 4 + 1 + 4 out of place (and 20/4 = 5)

As a few other examples:

Has a value of:

Since all the numbers are right where they belong. And:

Has a value of

Because 1 + 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 and 2/4 = 0.5

 

Your first reaction to solving this program might be toward a lookup table of some sort like I used with the Romania heurstic. But the challenge is that this is a very different problem. For example, I have seen students write something like this:

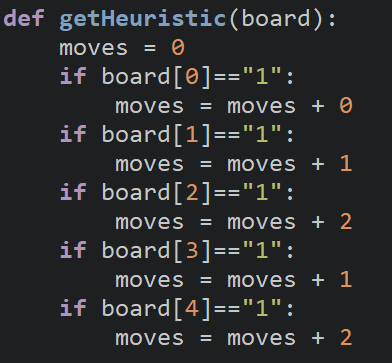
To do this requires 9*9 or 81 conditionals. That should scare the heck out of you. It can be done. But it is filled with opportunties to make serious errors, not to mention just SUCKS.

However, there is a really clean way to do this using integer division and modulo which converts the one-dimensional index number to a two-dimensional coordinate number.  I strongly encourage you to play with finding this algorithm. Think carefully about how you could take a position in the board (a number from 0-8) and convert it to a row (0-2) and a column (0-2) using integer division and modulo (remainder) arithmetic

board position = 0
row = 0
column = 0		 board position = 1
row = 0
column = 1		 board position = 2
row = 0
column = 2
board position = 3
row = 1
column = 0		 board position = 4
row = 1
column = 1		 board position = 5
row = 1
column = 2
board position = 6
row = 2
column = 0		 board position = 7
row = 2
column = 1		 board position = 8
row = 2
column = 2

 

 

My solution for comparison to your solution [or after you get so stuck you need help getting unstuck]

Again, how you use this is completely up to you and what learning outcomes you want. But here is my solution:

 

 

The Node class

When you are convinced your Heuristic is working correctly

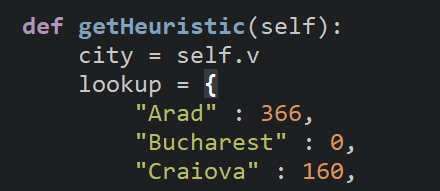
  1. Add this into the Node class and modify it so that rather than taking the board as a parameter it uses self.v as the board used in the calculation.
    • This function will give us the heuristic estimate needed as half of the fValue() function

  2. Notice that this particular problem didn't yet pay attention to costs so far - which is the number of moves made in the game.
    • Modify the constructor (__init__) to take in costSoFar as a fourth parameter and save this as self.cost (or self.c like in the Romania example)

  3. Add in the fValue() function that returns the sum of self.cost (or self.c depending on what you named it) and self.getHeurstic()
    • Hint, this is almost identical to the fValue function from the Romania problem.

  4. Add in the three magic methods we will use:
    • __lt__ [which is < ]
    • __gt__ [which is > ]
    • __eq__ [which is == ]

 

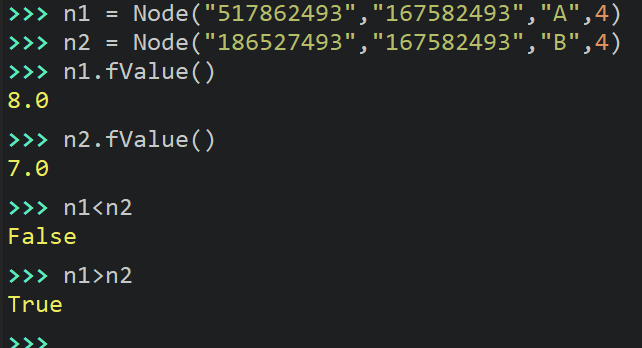
When you are all done with this you can test this by doing something like

 

 

Modify the search

If you get this far, the rest is EASY.

Using your previous Twiddle solution, modify the BFS search to be an A* search.  This requires:

Seriously. That's it. Now you should be able to run a search on a larger board in MUCH faster time.

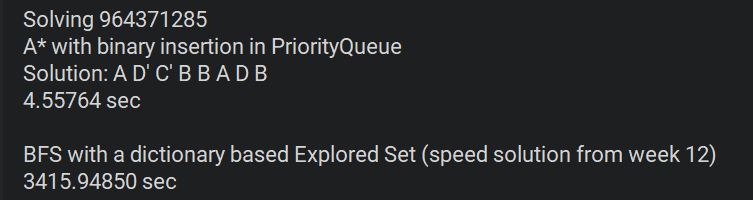
As an example this is what I got when I compared a length 6 solution board using my A* and the optimized BFS.

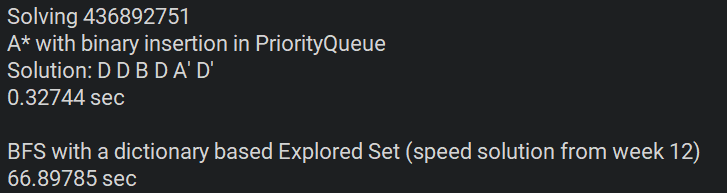
Notice how much more pronounced this is with a depth 8 solution. [And notice it was 4.5 seconds versus almost an hour]: