Implementing a Breadth First Search
Due: Sunday, November 6, Midnight
Introduction
Twiddle is a simple puzzle game we have been looking at for the last few weeks.

Tiles in the grid can be moved by rotating a group of tiles around one of the four interior intersection points. For the purposes of this assignment we will label those points as A, B, C, and D as indicated below:
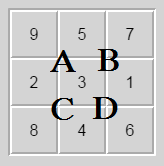
Notice that each of those rotation points touches exactly four tiles. The four tiles around each an intersection point can be rotated either clockwise or counter-clockwise around that point. For example, starting with this board:

rotating clockwise around point A would produce:

while rotating counterclockwise around point A would produce:

The goal of the game is to make a series of moves so that the numbers in the puzzle are in order as in the following:

From its starting point this sample puzzle can be solved in nine moves. If you want to give it a try you can attempt this puzzle by visiting sample puzzle #1 (note, a normal mouse click is a counter-clockwise rotation around the clicked point while a right click is a clockwise rotation). The optimal, nine move solution is available here if you can't figure it out and want to see how it works.
For this assignment you should write a program that will solve a Twiddle board using a Breadth First Search
Requirements
- Your code should be written in Replit as part of
- In the main.py file that is in that activity:
- complete the body of the function called BFS()
- that takes in a single, length 9 string as a parameter
- You CAN ASSUME this this contains one each of the numbers 1-9.
- There will be no spaces or punctuation.
- For example, the board used above as an example would be entered as "957231846".
- and prints the sequence of moves that will solve this puzzle (see below for the format)
- You should implement the Breadth First Search strategy for the generic search code as we have been discussing at the meetup and in the lecture videos:
- When a solution is found you need to print out the sequence of moves that will get you from the initial state to the goal state.

Your code needs to run in a "timely" manner. My first solution to this program (in python) had some time issues. A basic six move puzzle was taking 15-20 minutes to solve. After I made some revisions I can solve an eight move puzzle in 15-20 seconds and the nine-move puzzle above in about 45 seconds. If your code does not return a solution to an 8 move puzzle in under one minute I will consider that it has failed to satisfy this assignment EVEN IF it would work if I left it to run indefinitely.
From experience
- As you begin testing your solution make sure that it works on simple one move solutions. If your code can't quickly solve a board that only needs one move than you CERTAINLY can't solve deeper solutions. The following boards all are solvable with ONLY one move:
- 413526789 #A'
- 253146789 #A
- 152463789 #B'
- 136425789 #B
- 123746859 #C'
- 123586479 #C
- 123485796 #D'
- 123469758 #D
- Once you have those working move up to a few solutions of only two moves. Again, if your code can't find a solution to these boards almost instantly (no more than 2 seconds) than you have a larger issue:
- 236154789 #B A
- 142763859 #B' C'
- 413582796 #D' A'
- Once you master those then you can test the deeper boards. Here are a few other boards of particular depths:
- Recognize that it takes my code a minute to solve the 8 move solutions. Depending on how efficient you are with your own coding it may take that or more.
- You will want to think carefully about what you are asking any data structures to do and the Big-O notation for any searching and locating. By changing one of my data types from a list to a dictionary I was able to trim SIGNIFICANT time from my solution.
4 moves 6 moves 8 moves
239654178 436892751 287416935 185372649 675381429 147289356 461293587 361547289 938254671 234718956 486152739 964371285