CS 3540: Programming Languages and Paradigms

Session 14
An Application of Structural Recursion: A Small Interpreter

Opening Exercise: Variable Binding

An unused variable is a formal parameter that is declared by a function but never used in the body.

List the unused variables in each of these little language expressions: 

(f x)                      (lambda (x)
                              y)

(lambda (x)                ((lambda (x) x)
  (f x))                    (lambda (x) y))
        
                           (a
                            (lambda (z)
(lambda (x)                   (lambda (y)
  (lambda (x)                   (lambda (x)
    x))                           x))))

For more practice, try writing a function named (unused-vars exp) to solve this problem for you. Writing such a function may help you understand the idea of used and unused variables better. It is also good practice for Quiz 2.

These are fine test cases for Problem 4 on Homework 6.

a 2x2 comic strip panel. The upper left is Pooh dipping his hand into a honey jar. In the upper right, Tigger says, 'Sweet Jesus, Pooh! That's not honey.' In the lower left, Tigger says, 'You're eating recursion.' The lower right panel is an image of the full 2x2 comic, recursive in the lower right panel.
Pooh thinks recursion is tasty. I do, too.

Yesterday, Today, Tomorrow

Where We've Been

For the last few weeks, we have been discussing different techniques for writing recursive programs, all based on the fundamental technique of structural recursion. Last time, we applied these techniques in writing a recursive program to answer this question about programs in our little language from Session 12: Does a particular variable occur bound in a given piece of code? Our program, (occurs-bound? var exp), was mutually recursive with the function occurs-free? because the definitions of bound and free occurrences are mutually inductive.

In order to think and write more clearly about the little language, we used a new design pattern, Syntax Procedures, which allowed us to focus on the meaning of our data rather than their implementation in Racket.

Where We're Going

The next two units of the course explore important concepts in the design of programming languages, syntactic abstraction and data abstraction, by adding features to our little language and writing Racket code to process them. But our little language is so simple that it can be easy to lose track of where we are heading: the ability to write an interpreter for a programming language that actually does something.

Where We Are

Today, we use some of the ideas we have learned about Racket and recursive programming to implement an interpreter for a small language that actually does something, however simple. This trip has three goals: First, along the way, we'll see how we can begin to use the techniques we've been learning to write larger programs. Second, we'll see ways in which the things we will learn over the next few weeks fit into a language interpreter. Finally, we'll even take a few short breaks to have you write functions of your own, as practice.

The Cipher Language

Cipher is a simple language for encoding text. It has a one unary operator and two infix binary operators: 

(rot13 "Hello, Eugene")
("Hello, " + "Eugene")
("Eugene" >>> 3)
("Eugene" <<< 4)

I have written a function named value that evaluates Cipher expressions. The parentheses in Cipher make it easy to pass a Cipher expression to the function as a Racket list: 

$ racket
Welcome to Racket v8.5 [cs].
> (require "cipher-v1.rkt")
> (value '(rot13 "Hello, Eugene"))
"Uryyb, Rhtrar"

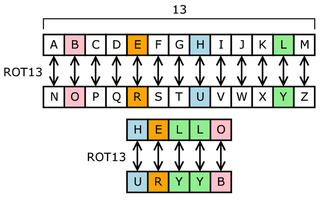
The rot13 operator implements a simple substitution cipher that replaces each letter with the 13th letter after it in the alphabet (mod 26):

a graphical demonstration of letter swaps in ROT-13
Source: illustration on Wikipedia's ROT13 page

This is the grammar for the Cipher language: 

exp ::= string
      | ( unary-op exp )          ; unary
      | ( exp binary-op exp )     ; binary
      | ( exp mixed-op number )   ; mixed

All values are strings. Numbers are literals in programs.

These are the operators I've defined thus far:

Here is the evaluator working on the other examples from above: 

> (value '("Hello, " + "Eugene"))
"Hello, Eugene"

> (value '("Eugene" <<< 4))
"Euge"

> (value '("Eugene" >>> 3))
"ene"

I considered including a (exp in exp) expression, but then we'd need boolean values, too. Let's keep things simple for a one-day excursion.

Let's examine the Cipher interpreter, value.

Syntax Procedures

My first job, before writing the interpreter itself, was to implement syntax procedures.

Look at the top of the file, including the provide clause and the (exp?) and (unary?) functions.

Quick Exercise: The mixed? Predicate

Write a structurally recursive function named mixed?.

This function takes one argument, which can be any Racket value. It returns true if that value is a mixed Cipher expression, and false otherwise.

A mixed expression has the form ( exp mixed-op number ), where mixed-op is <<< or >>>.

For example: 

> (mixed? '("Hello, Eugene" <<< 3))
#t
> (mixed? '(("Hello" >>> 4) <<< 3))      ; handles nested expressions
#t

> (mixed? 2)                             ; not a list
#f
> (mixed? '("Hello" >>>))                ; list not long enough
#f
> (mixed? '("Hello, Eugene" >>> "3"))    ; second arg not a number
#f
> (mixed? '("Hello, Eugene" slice 3))    ; not a valid operator
#f
You may assume that we have already implemented the general type predicate exp?.

Check out one solution in the syntax procs file. Rather than write an or expression to check the operator against all the possibilities, this code uses a little trick to make the code shorter: a member test. This approach also makes it easier to extend the language with new operators!

A First Look at the Interpreter

Take quick look at the rest of the syntax procedures:

Note: These functions have no knowledge of the meaning of the language. They know only about the syntax.

Now let's implement (value exp).

I have at least two options for writing the function:

Why did I choose helpers? The code is already complex enough, and as I add features to the language, the function will get even bigger. A monolithic function will be hard to read and hard to modify.

A compound example such as (("abc" <<< 2) + ("abc" >>> 2)) reminds us that we must evaluate any parts that are also expressions.

Quick Exercise: The eval-mixed Function

Let's implement one of the helper functions for value.

Write the function eval-mixed.

eval-mixed takes three arguments: a Cipher operator (a symbol), a string, and a number. The operator will be <<< or >>>. 

$ (eval-mixed '<<< "Eugene" 3)
"Eug"
$ (eval-mixed '>>> "Eugene" 3)
"ene"
You will want to use the Racket primitives (substring string start end) and (string-length string).

The choice in this function is between the two possible operators, so an if or cond is what we need.

A Second Look at the Interpreter

Let's look more at value and its helpers:

I could implement the one-operator functions without a cond expression, but using one...

There are many options for implementing the helper functions:

How to implement rot13: with a look-up table, or with math?

Once I had a working evaluator, I wanted to test and play more. Having to call value each time and quote the Cipher program became annoying. So I implemented a REPL for Cipher, named cipher, based on a Session 2 reading:

Adding a New Feature to Cipher—and the Interpreter

Option 1: Adding the Ability to Shift Strings

When doing this sort of string manipulation, we often want to shift strings like this: 

"Eugene" → "neEuge"
"abc"    → "cab"

We can do this now in Cipher using a compound expression: 

(("Eugene" >>> 4) + ("Eugene" <<< 2))
(("abc" >>> 2) + ("abc" <<< 1))

If we want to do this a lot, though, it would be nice if Cipher made it easier.

One way would be let users of Cipher write a function named shift and call it to perform this operation.

To do this, the Cipher evaluator would have to handle function definitions and function calls. We would have to extend the language grammar, and the interpreter, in several ways. That's too much work for a one-day excursion.

Another option would be to add a new operator to the language, (exp shift num).

Practice for home: Do it.

Implementing shift directly repeats other code in the interpreter. This is wasteful and prone to error. Many languages, including C++ and Racket, avoid this problem with a preprocessor.

We could do the same thing in Cipher: have the evaluator translate a shift expression into the equivalent Cipher expression using <<<, >>>, and + primitives, and then use existing machinery to evaluate it.

This is a powerful idea. We study it in detail in the next unit of the course, "Syntactic Abstraction". At that point, we can add a 'shift' operator to Cipher as an example.

Option 2: Adding Local Variables

Instead, let's add a simpler extension: names for primitive values, such as FIRST = "eugene" and LAST = "wallingford". (This is similar to how pi is a primitive value in Racket.)

To do this, we have to add variable references to grammar and update the other syntax procedures to work with them. We also need the ability to look up the value associated with a name.

That last part, you can do...

Quick Exercise: A lookup Function

Write a structurally recursive function named (lookup sym lop).

lookup takes two arguments, a symbol sym and a list of symbol/value pairs lop. 

$ (lookup 'w '((e . "Eugene") (w . "Wallingford")))
"Wallingford"

$ (lookup 's '((e . "Eugene") (w . "Wallingford")))
[error]

If you'd like to see recursive solution, check out this file.

Bonus Section: Interpreter, Version 2

We do not cover this session in class. Feel free to read the notes and the code, if you'd like. If not, no worries: nothing in this section will be on the quiz.

To add primitive variable references to Cipher, we need a new idea for our interpreter: the idea of an environment. An environment is a data structure that associates names with values. We then use a lookup function to find a value given a name.

Implementation of the environment: a list of symbol/string pairs. I also use a new-to-us primitive Racket function: assoc. It behaves similarly to the lookup you just wrote.

We have to make some changes to the value function:

With these changes, Cipher supports named values.

Wrap Up