CS 3540: Programming Languages and Paradigms

Opening Exercise: Standard Functions

Recap: Programming with Higher-Order Functions

For the last couple of sessions, we have been trying out a new way to write programs: asking functions to do more work for us. We found that apply and map will do a lot of work for us, if only we supply them with a helper function.

The purpose of map is to process all the items in a list in the same way:

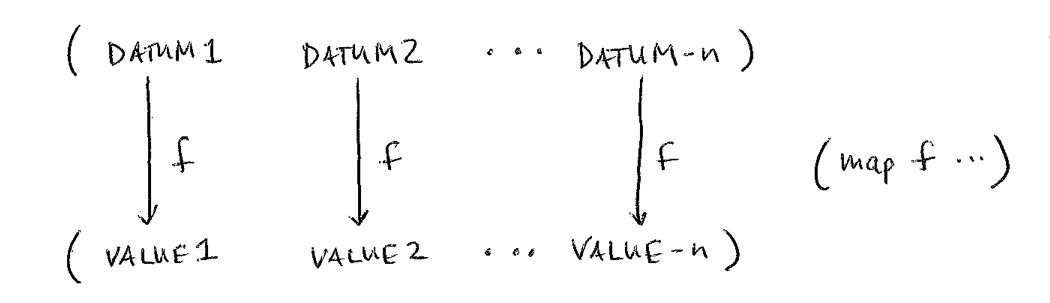
The purpose of apply is to combine all the items in a list into a single value:

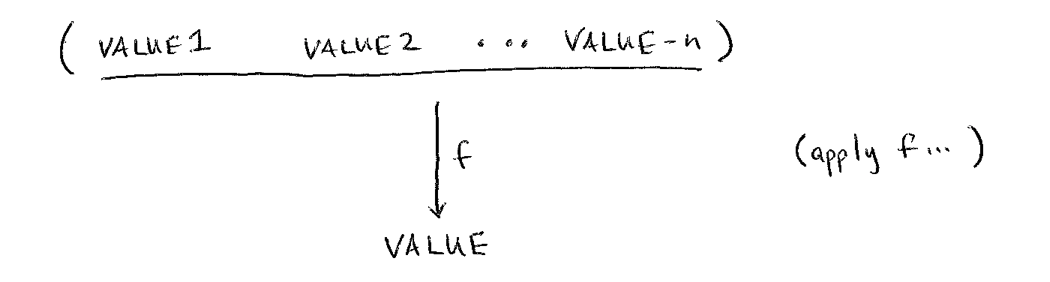
Used together, they create a powerful design pattern for solving an entire class of problems:

(apply reducer
       (map item-function
            list-of-values))

Why is programming this way such a challenge for you? You are used to thinking about problems in a different way. When you encounter a problem to solve, you start thinking about it — breaking it down into parts, solving the parts, putting the parts back together — in a particular way. These are habits you have learned and practiced for at least a couple of semesters.

Changing your mindset to a functional approach requires you to establish new habits and to break old ones. Creating new habits is a challenge, even when we want to change.

I know that many of you are not asking to change habits, or develop a new programming style. But it will make you a better programmer, and it will prepare you for something that is happening in industry right now. Give it a try, and you will be surprised.

One thing we can do when we are trying to break old habits and create new ones is to watch for the triggers that cause us to fall back into an old habit and have a plan for what to do instead. Let's solve a few more problems and observe the map-reduce pattern in action, include the variations we sometimes need.

Exercise: Computing a Department's Total Bonuses

This problem is a variation of a LeetCode problem, using data from the State of Iowa's salary book.

We start with salaries, a list of numbers: '(47599.2 93288.0 127940.0 ... 6731.2 139157.6).

Exercise: Computing a Department's Total Bonuses

It is more likely that we start with data in a spreadsheet or a database containing one records for each employee. Suppose we are given salary-list, a list of records that look like this: (county-name salary travel-expenses).

Exercise: Computing Maximum Average Daily Wind Speed

This problem is a variation of another LeetCode problem, using weather data from the Iowa Environmental Mesonet, a wonderful resource at Iowa State.

weather-data is a Racket list with data from a spreadsheet of daily weather data for Waterloo, Iowa, in 2024. Each day's record is of the form:

(
  city                 ; string (code)
  date                 ; string
  high-temp            ; number (Fahrenheit)
  low-temp             ; number (Fahrenheit)
  precipitation        ; number (inches)
  average-wind-speed   ; number (knots)
  snow                 ; number (inches)
)

Now you can see why we wrote a knots->mph function earlier!

Suppose now that we wanted to find the dates of the days that had this average daily wind speed. We might be able to solve that problem with map, but there is a better way.

A Style of Programming

From the last few sessions and Homework 3, we have been using a common programming pattern: map a function over a list, then apply a reducer to turn map's result into a single answer.

(apply reducer
  (map item-function
       list-of-values))

Our solution to Session 6's opening exercise does that:

(apply string
  (map first-char
       list-of-strings))

It processes a list of strings to create a list of characters and then reduces that list into a single string. Solutions to Problems 3 through 5 on the homework do something similar.

There are plenty of slight variations on this pattern. The two most common choices we face are:

• map a standard Racket function (say, Problem 3)
  or a custom function we write (say, Problem 4)
• apply a standard Racket function (say, Problem 4)
  or a custom function we write (say, Problem 3).

But there are others. Problem 5 required that we pre-process the list by dropping a header row with rest. On that problem, some of you found it convenient to do multiple map steps rather than write a more complex item function.

We are not limited by the pattern. It simply gives us a way to think about a problem and to structure our solution.

On first exposure, you might imagine that you'll never use functions such as map and apply after you finish this course, but you might be wrong... As noted last time, Google developed MapReduce to solve a common problem that arises when working with massive data sets. It is used widely in industry.

... O(n) and parallelism
... a visit to The Principal

Many of the functions we have been writing implement a simple form of MapReduce, using Racket's primitive functions. Next week, we will begin to learn techniques for writing other kinds of mappers and reducers.

Filtering a List

map is not the only way to process all of the items in a list. Sometimes we want to select all the items in the list that meet a given condition. For that task, we use the higher-order function filter:

(apply reducer
  (filter item-function
          list-of-values))

To find all of the days that positive numbers in a list, we can write:

(filter positive? '(0 2 0 0 3 0 9))

The function we give to filter is a boolean function. It returns true for the items we're looking for and false for the others.

Now let's return to our question about wind speeds.

To find the dates of the days that had the year's maximum average wind speed, we need to write a function that returns true for such days and false for the others:

(lambda (day-entry)
  (= (max-wind-speed weather-data)
     (knots->mph (sixth day-entry))))

With this function, filter can do the job:

(filter (lambda (day-entry)
          (= (max-wind-speed weather-data)
             (knots->mph (sixth day-entry))))
        weather-data)

To get a list of the dates themselves, rather than the entire records, a call to map is what we need:

(map second
     (filter (lambda (day-entry)
               (= (max-wind-speed weather-data)
                  (knots->mph (sixth day-entry))))
             weather-data))

We can use map outside of the map-reduce pattern, too.

Exercise: Finding Days Warmer Than Average

Let's return to our weather-data for Waterloo 2024:

(
  city                 ; string (code)
  date                 ; string
  high-temp            ; number (Fahrenheit)
  low-temp             ; number (Fahrenheit)
  precipitation        ; number (inches)
  average-wind-speed   ; number (knots)
  snow                 ; number (inches)
)

First, a quick warm-up:

How warm was it in Waterloo in 2024? The U.S. Climate Data website tells us that the average high temperature in Waterloo is 58° F.

Thinking Functionally

The patterns of data in our solutions look something like this:

MAP      from  (d1 d2 d3 d4 d5 d6 ...)
           to  (v1 v2 v3 v4 v5 v6 ...)

FILTER   from  (d1 d2 d3 d4 d5 d6 ...)
           to  (d1    d3       d6 ...)

APPLY    from  (d1 d2 d3  ...)
           to  n

You can create new habits, with attention and practice. Take baby steps. Use the REPL to help you build code you trust. Practice, practice, practice.

Wrap Up

• Reading
  • Nothing new. Review the notes for Sessions 1-7 along with any reading assignments given in them.
• Homework
  • Homework 3 was due last night.
• Quiz 1
  • The quiz comes at the end of Session 8, on Thursday. It will cover our readings so far and our in-class coverage of Racket and functional programming style. This includes:
    • Racket's built-in data types (primitives) and functions
    • Racket expressions (means of combination) and data structures
    • Racket definitions and functions (means of abstraction)
    We have paid special attention to Racket functions and how they differ from functions in other languages.
  • I don't write study guides, but... Most sessions have an orientation section near the beginning, sometimes with a header like "Recap" or "Where Are We?". Today's is called Recap: Programming with Higher-Order Functions. These may help you see the terms and ideas we have been studying. And the items listed as the reading assignments each day are important, especially the short sections I wrote for you.