Paired Programming Activity
Loop Problems, part 1

Activities

I would like you to attempt to complete several small Python functions working with your partner.

Please try to make your program output look as much like the example as possible and verify it works with the example input provided. If you have difficulty finding the information or understanding how to approach the problem, you should contact me.

To complete this activity, you will need to create the following scripts:

• LOOP 0 - discountTable() [Not submitted to Autolab but you should do it]
• LOOP 1 - collatz()
• LOOP 2 - howLong()
• LOOP 3 - finalPopulation() [Challenge Problem]

LOOP 0

Santa put Kohls in your stocking

If you have ever shopped at one of those stores like Kohls that seems to have CONSTANT sales, you will now that they often have signs showing you the original price of the item and the sales price of the item.  If there are lots of items with different prices they will often print a table of multiple items.

Write a Python function that conforms to the following:

• Function name
• discountTable()
• Parameters
• A (lower) starting Price (must be an integer)
• A (higher) ending Price (must be an integer)
• An interval between prices (must be an integer)
• A % off discount (could be a float)
• Return value
  • Nothing.
  • This is what is known as a "non-fruitful" function. It doesn't produce results in the traditional sense. Instead it prints inside of the function.
• So what does it print:
  • The function should print a table of all the original price and the sale price for all amounts in the interval defined by the first three parameters.
  • Place three spaces between the two "columns"
  • Round the prices to 2 decimals (Remember, that this won't add decimal places. Just remove them)
  • Include $ symbols as shown.
  • NOTE, this will only work if your printing matches mine EXACTLY.
• Examples
• 

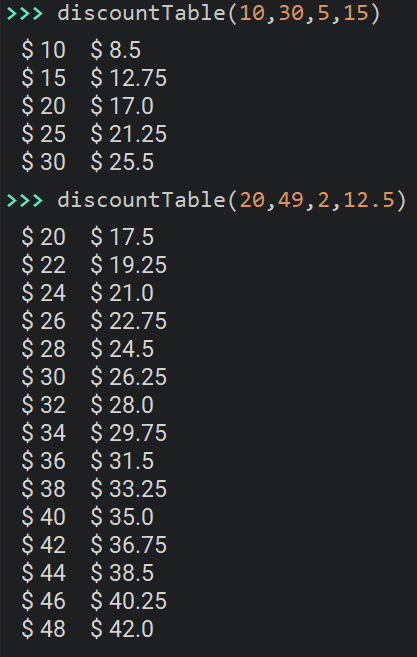
Note: Autolab does not handle programs like this well. But it's still a really good activity. Take time to make sure you get outputs like those given above and then test with a few additional sets of parameters to confirm that your code appears to work correctly.

LOOP 1

I have a conjecture

According to Wikipedia, "The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two sipmle arithmetic operations will eventually transofrm every positive integer into 1." It is named after mathematician Lothar Collatz who first introcued the idea in 1937

The process is as follows:

Then you continue this process on the new number repeatedly until you finally arrive at the number 1.

For example:

In other words, it took us 7 moves to go from 3 to 1.

While it hasn't been officially proven yet, Collatz has proposed that EVERY positive integer will eventually work its way to 1.

Write a Python function that conforms to the following:

• Function name
• collatz()
• Parameters
• A positive integer
• Return value
• The number of moves it takes to go from the starting parameter to 1
• Examples
• 

 

LOOP 2

TC Works for the UNI Foundation

TC has started working for the UNI Foundation.  One of the ways that UNI is able to give scholarships is off of the interest from smart, long-term investments.  They are trying to figure out how long it will take them to double their money in particular investments.

• Function name
• howLong()
• Parameters
• An initial investment
• The annual interest rate (put in as a percentage such as 5 or 2.75)
• Return
• The number of years needed until the investment is worth at least twice as much (how long until it has doubled?)
• Examples
  • 

NOTE: This is a loop problem. You must use a loop to get credit. DO NOT simply use a formula.

LOOP 3

It's a Growing Problem

NOTE: This is a challenge problem.
I think it is a great example of a basic loop problem.
BUT, the math in it is a bit tricky and requires you to put together some things we have done in very different ways.
The challenge isn't the loop - it's the math that controls the loop. I encourage you to give it an honest try and then
watch the video to see how I would solve it.

Steph Infection is a biologist who is studying the generation time of various bacteria.

In biology the generation time is the time it takes for a population to double in size. For example, when E Coli bacteria are placed in a favorable medium, such as Glucose salts, they have a generation time of approximately 20 minutes.

Steph wants to be able to calculate how many bacteria she should expect to find in her petri dishes after a certain amount of time.

• Write code that asks the user for:
  • The starting size of the bacteria culture
  • The generation time of the bacteria (assumed to be in minutes)
  • How much time will elapse (assumed to be in hours)
• The program will then
  • Calculate how many generation intervals have occured.
  • Round to the nearest interval number
  • Calculate and print how many bacteria are in the final sample

Write a Python function that conforms to the following:

• Function name
• finalPopulation()
• Parameters
• The initial size of the bacteria culture
• The generation time of the bacteria in the culture (assumed to be in minutes)
• How much time will elapse (assumed to be in hours)
• Return value
• The number of bacteria expected in the final sample
• Examples
• 
• Special Notes
• This is a looping problem where every time through the loop the population doubles. You should be using a loop and not a single mathematical formula to calculate the results.
• You will have to determine how many "generations" occur during the time elapsed so you know how many times to run the loop.
  • For example, a 20 minute generation time over 3 hours (180 minutes) is 9 generations.
• If the number of generations isn't an integer you should ROUND to the nearest integer
  • For example, a 17 minute generation time over 3 hours is 10.588 generations which we will round to 11
  • As another example, a 16 minute generation time over 3 hours is 11.25 which we will also round to 11