Week 8 - Recursive Algorithms

Outcomes

You should be able to:

• Describe the three "laws" of recursion.
• Identify where each of the three "laws" of recursion are observed in a recursive algorithm.
• Identify the Big-oh runtime analysis for a recursive algorithm.

Activities

Getting Started

• Watch - What is this thing called recursion? [Video - 13 minutes]
• Watch - How recursion was used in Fractal Ferns [Video - 5 minutes]
• Watch - How recursion was used in the Sierpinski Triangle [Video - 5 minutes]
• Watch - How recursion was used in the Code.org Binary Search algorithm [Video - 8 minutes]
• Watch - How recursion was used in the textbook Binary Search algorithm (the better one in my opinion) [Video - 6 minutes]

Reading

• Section 4.2 - What is Recursion?
• Section 4.3 - Calculating the Sum of a List of Numbers
• Section 4.4. The Three Laws of Recursion
• Section 4.5. Converting an Integer to a String in Any Base
• Section 4.6. Stack Frames: Implementing Recursion
• Section 4.7. Visualizing Recursion
• Section 4.8. Sierpinski Triangle
• You may read 4.10 and 4.11 based on your interests

Some additional examples

• Writing/viewing a few recursive algorithms
  • Watch - isPalindrome() [Video - 13 minutes]
    • Finished Recursive Code
    • Non-recursive algorithms using loops (two versions)
  • Watch - Recursive Sudoku [Video - 13 minutes]
    • Sudoku Code

You Try It

In this activity I would like you (with a partner if you like) to try to use what you just learned to create recursive algorithms in python for:

• Finbonacci
  • Recall that the Fibonacci sequence is:
    • 1,1,2,3,5,8,13,21,34,55,...
  • The first two numbers are 1 and then
  • Each number is the sum of the two numbers before it:
    • Fib(n) = Fib(n-1) + Fib(n-2) when n ≥ 3
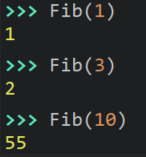
• Write a function called Fib() that takes in a positive integer and returns the value at that position in the Fibonacci sequence. For example:
  • 
• NOTE: This algorithm is a classic one that teachers talk about to WRITE the algorithm because it is really short/simple. BUT, it is not an algorithm we woud ever "deploy" because it's runtime is O(2ⁿ) or exponential. Yes, you read that right O(2ⁿ) and not O(n²). Big difference.
• Even if you figure out how to write this algorithm, I encourage you watch the followup video below to see what I mean by this.

 

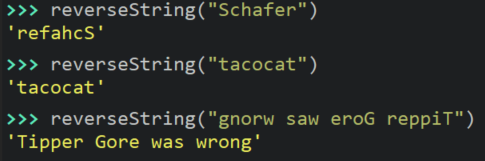
• Reverse a string
  • One way to reverse a string is to understand that the first letter of the string needs to be moved to the back of the string
  • And once you do that, you need to take what is left and move the first letter of THAT to the back of the sub-string
  • and so on
  • and so on
• 
• For example:
  • 

You Try It Solutions

• Watch - My explanation for the Fib() code [Video - 4 minutes]
  • recursive_finoacci.py - the code in that video
• Watch - My explanation about why recursive Fib() is O(2ⁿ) or Exponential and is AWFUL. [Video 6 minutes)
• Watch - My explanation of reverseString [Video - 4 minutes]
  • recursive_reversal.py - the code in that video