Activity 1 - Searching for a solution to Twiddle

Last week we looked at the very introduction of "Intelligent Search" - that is, how to search for a solution to a problem. We looked at two search techniques - Breadth-First Search and Depth-First Search - and on two different problems - the Analysts/Hackers Canoe problem, and the Romanian Map prolbem. During that time we looked at the code that could be used to search for solutions to these problems and how the key thing you have to create in this is not so much the search algorithm itself - that is pretty straight forward - but the code to store nodes and generate new children nodes.

Today I want to give you a chance to try your hand at programming one or two of these problems for yourself. I know that as soon as I say "I am not collecting this for a grade" a large number of you will skip it. But I actually hope that you really do explore these problems EVEN if you only spend an hour doing it and then look at the published solution. Because I think there is something that all of you can gain - even the elementary teachers - by exploring.

Watch - Introducing Twiddle [Video - 6 minutes]

Introducing Twiddle

Twiddle is a simple number puzzle played on a 3-by-3 grid. On first glance it might look like the plastic "sliding 8 puzzle" that you might have played as a kid where the numbers 1-8 are in a grid with one empty space:

While similar in looks, Twiddle has a very different set of movements and a related but different goal. Twiddle starts with all 9 numbers in the 3x3 grid and the goal is to move the 9 pieces until they are in order:

You will notice that there isn't a blank space here. So how do the pieces move? In this puzzle, four of the nine pieces move together by rotating them around their shared corner. For example, 2, 6, 1, and 9 all meet at a shared corner. 6, 5, 9, and 3 all meet at a second shared corner. Notice that there are 4 of these shared corners that we will label as A, B, C, and D.

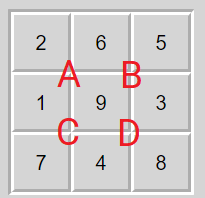
The four pieces at a shared corner can be rotated either clockwise, or counter-clockwise around their shared corner. So from the opening puzzle above we have two results from rotating around A

Clockwise around A	Counter-clockwise around A

Notice that 5, 3, 8, 4, and 7 stay the same with both of these moves. The only 4 that move are the 4 around the rotation point.

To play with this puzzle you can go to:

https://www.chiark.greenend.org.uk/~sgtatham/puzzles/js/twiddle.html#3x3n2:2,6,5,1,9,3,7,4,8

On a PC you use the left mouse (or the left side of the trackpad) to rotate to the left (counter-clockwise) and the right mouse button (or the right side of the trackpad) to rotate to the right (clockwise). Explore the link above to see how the puzzle pieces move. Can you solve it? [This one is much easier than most. This puzzle can be solved with only three moves]

To explore truly random puzzles you can use

http://www.chiark.greenend.org.uk/~sgtatham/puzzles/js/twiddle.html

Think of the Children

I have already alluded to the fact - actually, no, I have flat out STATED - that the biggest issue you will face if you wanted to make your own programs to perform various search techniques like we have been studying will probably be the issue of generating children. So let's have you spend some time working on this with a partner

Quick Question - Given any Twiddle board, how many chidren does it have?

Discuss that with your partner(s).

When you think you have the answer...

Watch - How many children in the Twiddle problem [Video - 5 minutes]

YTI Activity

• Get together with a partner.
• Download the following two python files to the same location
  • twiddle.py
  • children_checker.py
• Open children_checker.py
• Write the code for the children() function so that it
  • that takes in a single, length 9 string as a parameter
  • and returns a list of 8 strings. 
• Each of these should be one of the children of the original parameter twiddle board.
• For sake of helping with feedback, please put these in the following order of moves:
  • [ A, A', B, B', C, C', D, D']
  • where the prime version is counterclockwise and the regular version is clockwise
• For example:
  • 
• Another example:
  • 

When you think you have it you can test that I agree with you by opening and running children_checker.py. If it is correct you will see:

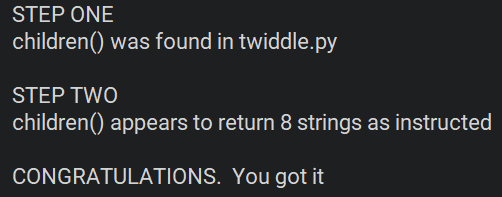
If not, look carefully at the messages and try to debug.

Solution Variations

Once you have a solution to children(), or you decide you just aren't going to get it to work, I encourage you to explore three variations to this problem to see how they work.

• Common solution using strings
• Less common solution using lists
• "Streamlined" solution

I will post a walkthrough video for this solution the week after the CoP event. The goal is to have you explore these solutions on your own first.