Continuity correction factor
Because the normal distribution can take all real numbers (is continuous) but
the binomial distribution can only take integer values (is discrete), a
normal approximation to the binomial should identify the binonial event "8"
with the normal interval "(7.5, 8.5)" (and similarly for other integer values).
The figure below shows that for P(X > 7) we want the magenta region
which starts at 7.5.
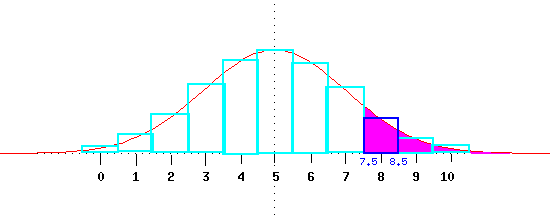
Example: If n=20 and p=.25, what is the probability that X is greater than
or equal to 8?
- The normal approximation without the continuity correction factor yields
z=(8-20 × .25)/(20 × .25 × .75)^.5 = 1.55, hence P(X
*greater than or
equal to* 8) is approximately .0606 (from the table).
- The continuity correction factor requires us to use 7.5 in order to include
8 since the inequality is weak and we want the region to the right.
z = (7.5 - 5)/(20 × .25 × .75)^.5 = 1.29, hence the area under the
normal curve (magenta in the figure above) is .0985.
- The exact solution is .1019
approximation
Hence for small n, the continuity correction factor gives a much better answer.
Competencies: Use the normal approximation with the continuity correction factor to approximate the probability of more than 40 successes if n=60 and p=.75.
return to index
Questions?
