Venn diagrams and algebra of sets
We shall employ the notions of intersection, union, and complement of a set,
which is best illustrated with a Venn diagram.
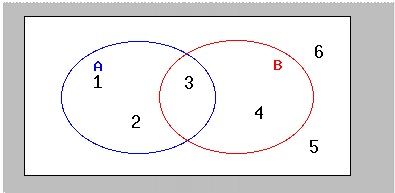
Click here for Venn diagram in ascii.
In this Venn diagram:
- S={1, 2, 3, 4, 5, 6} (the sample space or universal set)
- A={1, 2, 3} (everything in the circle labelled A)
- B={3,4} (everything in the circle labelled B)
- A'={4, 5, 6} (A-complement, equivalent to S\A or S-A, everything in the
sample space which is not in A; I prefer a superscript c to denote complement,
but do not have that type-setting option)
- B'={1, 2, 5, 6}
- AB={3} {A intersect B, also written with an inverted U between the A
and B, everything that is in both A and B)
- AUB={1, 2, 3, 4} (A union B, the U should be san serif and perhaps
smaller than the type font (it is not really a U))
To see these regions graphically, click here (ascii version not available).
More definitions and results for the algebra of sets is available at C.Mosier.
return to index
Questions?

