Test of hypothesis (one-tail)
A two tailed test of hypothesis tests the null hypothesis H0 (the 0 should be
a subscript) that the mean is a specified value (µ =
39 in the previous example) against the alternative hypothesis HA (the A
should be a subscript) that the mean is not equal to that value (µ is not
equal to 39 in the previous example). You reject the null hypothesis if
x-bar is too large or too small.
Sometimes the null hypothesis is that the mean is at least (or at most) a
specified value. (e.g., there are at least two scoops of raisins in Kellogg's
Raisin Bran, there are at most 5 ppm lead in drinking water.) In this case
one would reject the null hypothesis only if x-bar is too small (or too large,
respectively). In this circumstance a one-tailed test is employed. The null
hypothesis (H0) for a one tailed test is that the mean is greater (or less)
than or equal to µ, and the alternative hypothesis is that the mean is
< (or >, respectively) µ. The text will always use = to state the
null hypothesis, and use the alternative hypothesis to identify whether it
is a one-tailed test, and which tail. Often a subscript 0 will be appended
to µ to emphasize that it refers to the mean under the null hypothesis.
Examples:
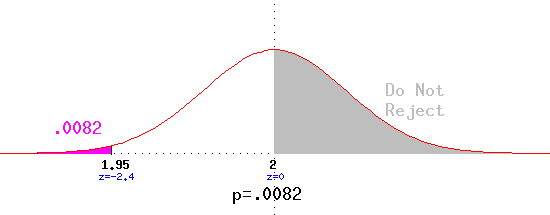
- If x-bar based on 144 boxes of Raisin Bran is 1.95 scoops of raisins
and you know that the standard deviation for the number of scoops of raisins
is .25, do you reject that there are two scoops of raisins in Kellogg's Raisin
Bran?
z = (1.95-2)/(.25/12) = -2.4. The area associated with the z-value -2.4 is
.0082. Since 1.95 < 2, you might reject the null hypothesis; since it is
a one tailed test, p=.0082. Therefore, you reject the null hypothesis at
the 1% significance level, but fail to reject it at the .005 significance level.
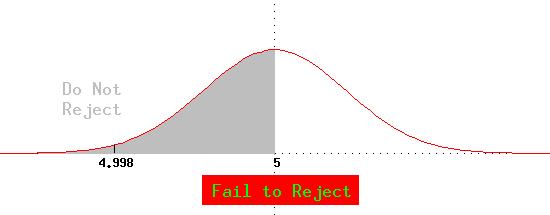
- If based on 100 samples you find 4.998 ppm lead in water, and you know
that the standard deviation of ppm lead between samples is .005, do you
reject that the lead level is less than 5 ppm?
Because 4.998 is consistent with the null hypothesis (µ is less than or
equal to 5 ppm), hence inconsistent with the alternative hypothesis (µ
> 5 ppm); you do not reject the null hypothesis.
Competencies: If the standard deviation is known to be equal to 12, and your null hypothesis is that the mean of the population is less than or equal to 15 i.e., the alternative hypothesis is that the mean is greater than 15, at what level (p-value) is x-bar = 13.5 based on a sample of size 200 significant? Would you reject the null hypothesis at the 10% significance level? 5% significance level? 1% significance level?
If the standard deviation is known to be equal to 12, and your null hypothesis is that the mean of the population is greater than or equal to 15 i.e., the alternative hypothesis is that the mean is less than 15, at what level (p-value) is x-bar = 13.5 based on a sample of size 200 significant? Would you reject the null hypothesis at the 10% significance level? 5% significance level? 1% significance level?
Reflection: How are one and two tailed tests related? Where in the calculations is the one- or two-tailedness of the test manifested?
return to index
Questions?

