Graphical Display of Qualitative Data

The data which statisticians collect has been classified as nominal, ordinal, interval, and ratio. Nominal data has the least inherent structure, it is data such as the color or flavor of jelly beans. All a statistician can do is count how many beans are of each color. Ordinal data is data such as egg size (small, medium, large, or extra large); all a statistician can do is count how many eggs are of each size, but there is a natural way to present the results (from small to extra large). Nominal and ordinal data are sometimes collectively called categorical or qualitative data. There is no natural way to identify categorical data such as red and green or small and large with real numbers, hence statistics such as the mean cannot be calculated. The only sense of "average" which can be found for categorical data is the mode, which is the most frequent category.

One means to display categorical data is with a bar chart. Several parallel bars are used, with the height of each bar proportional to the number of data in each category. For example, if one had 4 apples, 7 bananas, 5 guavas, 3 mangos, and 6 pears, the information could be displayed thus:


       |          ___
       |         |   |                 ___
     5_|         |   |   ___          |   |
       |   ___   |   |  |   |         |   |
       |  |   |  |   |  |   |   ___   |   | 
       |  |   |  |   |  |   |  |   |  |   |
       |  |   |  |   |  |   |  |   |  |   |
       |__|___|__|___|__|___|__|___|__|___|__
            A      B      G      M      P

          Frequency of Fruit Selections

Note that it is necessary to label the bar graph to convey information, in particular the number of fruit is indicated on the vertical axis. Alternatively, one could record the relative frequency of each type of fruit in which case the actual number of each type of fruit could not be read from the bar chart. A relative frequency bar chart would look essentially the same, but the vertical axis would be labelled differently:


       |          ___
       |         |   |                 ___
   20%_|         |   |   ___          |   |
       |   ___   |   |  |   |         |   |
       |  |   |  |   |  |   |   ___   |   | 
   10%-|  |   |  |   |  |   |  |   |  |   |
       |  |   |  |   |  |   |  |   |  |   |
       |__|___|__|___|__|___|__|___|__|___|__
            A      B      G      M      P

       Relative Frequency of Fruit Selections

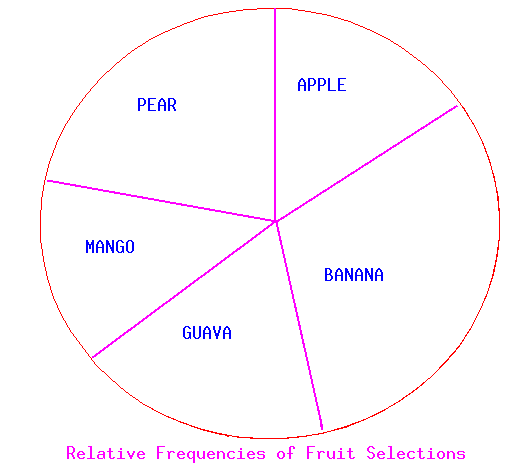
This information can also be displayed in a pie chart, which by its manner of display emphasizes relative freauencies (i.e., parts of the whole).

If one had a protractor (and the pie chart was accurately drawn), one could determine 16% of the fruit were apples, 28% were bananas, etc. Pie charts may also be labelled with more information including the actual counts.
lbelled pie chart

return to index

Questions?