Quartiles, boxplots, percentiles, and z-scores
In order to describe a data set without listing all the data, we have measures
of location such
as the mean and median, measures of spread such as the range and standard
deviation, and
descriptions of shape such as symmetric, skewed, unimodal, and bimodal. We can
also get a good
sense of the distribution of a set of data with five carefully chosen measures
of location. We
supplement the median, minimum, and maximum with the first and third quartile,
which indicate
the extent to which the data lies near the median, or near the extremes.
There are many definitions for calculating the first and third quartiles, which
definitions do
not all give the same results. Heuristically, one fourth of the data lies below
the first
quartile (hence three-quarters above it). Similarly, three quarters of the data
lies below the
third quartile (hence one quarter above it). The first and third quartiles are
the medians of
the lower half and upper half of the data, but whether or not you include the
median when there
are an odd number of data is one reason definitions vary. The second quartile
is by definition
the median.
Note that a quartile is a number or cutoff, and not a range of
values. One may
be above or below the first quartile, but not in the first quartile.
The five number summary, i.e., the minimum, Q1, Q2 (median), Q3, and maximum,
give a goo
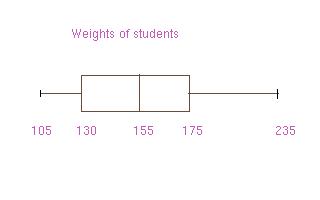
indication of where data lie. For the data set of weights The
five number summary is: 105,130, 155, 175, 235. One know immediately that half
the data is
below 155, half is above 155, and alternatively half is between 130 and 175.
The five number summary is sometimes represented graphically as a
(box-and-)whisker plot. The
first and third quartiles are at the ends of the box, the median is indicated
with a vertical
line in the box, and the maximum and minimum are at the ends of the whiskers. A
boxplot for
the weights is depicted below.
Exercise: How is a boxplot similar to a histogram? How is it different?
Percentiles are like quartiles, except that they divide the data set into 100
equal parts
instead of four equal parts (similarly, there are quintiles and deciles and
...). Percentiles are useful for giving the relative standing of an individual
in a population, they
are essentilaaly the rank position of an idividual.
As with quartiles, there are definitions which vary slightly specifying how to
calculate percentiles. One definition is the fraction of the population which
is less than the specified value.
If one wants to compare someone who
graduted 37th out of a class of 250 with someone who graduated 12th in a class
of 60, one can
calculate 213/250 = .852 which is rounded down to the 85th percentile
(percentiles measure position from the bottom, 37 from the top means that 213
are below it in a population of 250); similarly 48/60 = .80 or the 80th
percentile. Therefore, being 37th out of 250 puts one at the
85th percentile, which is better than 12th out of 60 which is only at the 80th
percentile.
Another way to compare individuals in different populations is with z-scores.
If mu is the mean
of a population s is the standard deviation, the z-score of a value x is
(x-mu)/s (note that
z-scores may be positive or negative). A standard example for demonstrating the
utility of
z-scores is comparing a score on the ACT tests with a score on the SAT tests.
Originally, SAT
tests had a mean score of 500 with a standard deviation of 100, while ACT tests
had a mean
score of 18 with a standard deviation of 6 (these are no longer the means and
standard
deviations for thosae tests). Hence one could compare 680 on the SAT with 25 on
the ACT. The
respective z-scores are (680-500)/100 = 1.8 and (25-18)/6 = 1.17. Therefore 680
on the SAT is
a better score than 25 on the ACT (assuming equal quality among the students who
took the two
tests).
Z-scores measure how outstanding an individual is relative to the standard
deviation for that
population. Note that percentiles use the median as the average (50th
percentile), while
z-scores use the mean as average (z-score of 0).
Competencies: For the data set {2 5 9 4 6 7 6 8 8}, calculate the
quartiles and 5-number
summary.
For the class weightsfind the percentile and
z-score of the 168
pound individual.
Reflection: When are z-scores versus percentiles a better measure of
relative standing?
Challenge:
May 2002
return to index
campbell@math.uni.edu

